Forth is a programming language that uses two stacks and a dictionary of words.
A Forth environment combines the compiler with an interactive shell, where the user defines and runs subroutines called words. Words can be tested, redefined, and debugged as the source is entered without recompiling or restarting the whole program.
Forth programmers enjoy the immediacy of an interpreter while at the same time the performance and efficiency of a compiler.

My principal forth environment is Felix Winkelmann's UF, a wonderful little graphical forth environment running on the Uxn virtual machine. I also sometimes use a custom version of the lbforth.c REPL, modified to work on Plan9(ARM) which can be downloaded here.
Basics
Forth reads from left to right, spaces are separators, when you wish to quit, type BYE. A stack is a way of managing data. With a stack, data is added to and taken from the "top", as with a stack of dishes. The acronym for this is LIFO: Last In First Out.
To inspect the stack, type .S
10 20 30 .S 30 20 10 OK DROP .S 20 10 OK BYE
Forth has no operator precedence, and does not need parentheses.
| Reverse Polish | Infix |
|---|---|
| 3 4 + 2 * | (3 + 4) * 2 |
| 2 3 4 * + | (3 * 4) + 2 |
| 2 3 * 4 + | (2 * 3) + 4 |
| 5 6 + 7 * | (5 + 6) * 7 |
Words
The dictionary comes with the Forth system. The programmer writes a program by adding to the dictionary words defined in terms of words in the dictionary. As a rule, Forth finds a word by starting with the most recently defined word and working backwards. If two or more words in the dictionary have the same name, Forth will find the most recently defined and be satisfied.
A colon definition starts with the Forth word :
: HELLO ." Hi! " ; HELLO Hi! OK
Because in Forth data is passed implicitly, it is considered insane to define a word without documenting what data it takes from the stack and what data it returns to the stack. The canonical way of doing this is to use the Forth word ( which tells the system to ignore what follows up to and including the next ). Expectations ("before") and results ("after") are separated by --. The resulting ( before -- after ) is a "stack-effect comment".
: SQUARED DUP * ; 5 SQUARED . 25
You program in Forth by teaching a machine new actions that you and the machine know by name. Each new action is a novel arrangement of known actions, perhaps mixing in some data. By being added to the dictionary the new action can be used to teach still newer actions.
: SQUARED ( n -- n**2 ) DUP * ; : CUBED ( n -- n**3 ) DUP SQUARED * ; : 4TH ( n -- n**4 ) SQUARED SQUARED ;
Logic
There’s actually no boolean type in Forth. The number 0 is treated as false, and any other number is true, although the canonical true value is -1 (all boolean operators return 0 or -1). Conditionals in Forth can only be used inside definitions.
The simplest conditional statement in Forth is if then, which is equivalent to a standard if statement in most languages. Here’s an example of a definition using if then. In this example, we’re also
using the mod word, which returns the modulo of the top two numbers on the stack. In this case, the top number is 5, and the other is whatever was placed on the stack before calling buzz?. Therefore, 5 mod 0 = is a boolean expression that checks to see if the top of the stack is divisible by 5.
: BUZZ? 5 MOD 0 = IF ." BUZZ" THEN ;
Loops
: STAR [CHAR] * EMIT ; : STARS 0 DO STAR LOOP CR ; 10 STARS **********
Stack Primitives
Stack machines are arguably the simplest kind architecture. Their LIFO structure is quite suitable for block-oriented languages. The code size for a stack machine can be very compact because most instructions have no operand field.
POPRemove an item at index, closing the hole left in the stack.ROLLRemove an item at index, push it on top of the stack.PICKCopy an item at index, push it on top of the stack.
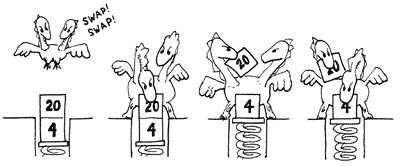
Given the Last In First Out stack a b c, here are the resulting stacks after each primitive:
| Primary | Secondary | Definition | ||
| POP | 0 | DROP | a b | Discard top item. |
|---|---|---|---|---|
| 1 | NIP | a c | Discard second item. | |
| ROLL | 0 | SWAP | a c b | Bring second item to top. |
| 1 | ROT | b c a | Bring third item to top. | |
| PICK | 0 | DUP | a b c c | Copy top item. |
| 1 | OVER | a b c b | Copy second item to top. | |
Minimal Forth Architectures
In The Road Towards A Minimal Forth Architecture, Mikael Patel builds toward a forth from only a handful of arithmetic and stack primitives. Here is an implementation of some of these primitives in Uxntal macros.
%t! ( v -- ) { .t STZ }
%t@ ( -- v ) { .t LDZ }
%r> ( | v -- v ) { STHr }
%>r ( v -- | v ) { STH }
%1+ ( x -- x+1 ) { INC }
%0= ( x -- flag ) { #00 EQU }
%nand ( x y -- z ) { AND #ff EOR }
%exit ( -- ) { BRK }
%minint { #80 }
%drop ( v -- ) { t! }
%dup ( v -- vv ) { t! t@ t@ }
%swap ( ab -- ba ) { t! >r t@ r> }
%nip ( ab -- b ) { >r t! r> }
%over ( ab -- aba ) { >r t! t@ r> t@ }
%tuck ( ab -- bab ) { t! >r t@ r> t@ }
%rot ( abc -- bca ) { >r >r t! r> r> t@ }
%2swap ( abcd -- cdab ) { >r t! >r >r t@ r> r> r> t! >r >r t@ r> r> }
%2dup ( ab -- abab ) { t! t@ t@ >r >r t! t@ r> t@ r> }
%2over ( abcd -- abcdab ) { >r >r 2dup r> r> 2swap }
%2drop ( ab -- ) { t! t! }
%3rev ( abc -- cba ) { t! >r t@ >r t! r> r> t@ }
%4rev ( abcd -- dcba ) { t! >r t@ >r t! r> r> t@ >r >r >r t! r> r> r> t@ }
%third ( abcd -- abca ) { >r >r t! t@ r> r> t@ }
%fourth ( abcd -- abcda ) { >r >r >r t! t@ r> r> r> t@ }
%3dup ( abc -- abcabc ) { third third third }
%not ( a -- b ) { dup nand }
%and ( a b -- c ) { nand not }
%or ( a b -- c ) { not swap not nand }
%xor ( a b -- c ) { over over not nand >r swap not nand r> nand }
%r@ ( | x -- x | x ) { r> r> dup >r swap >r }
%1- ( x -- y ) { not 1+ not }
%2+ ( x -- y ) { 1+ 1+ }
%2- ( x -- y ) { not 2+ not }
%negate ( x -- y ) { not 1+ }
%boolean ( x -- flag ) { 0= 0= }
%0< ( x -- flag ) { minint and boolean }
%0> ( x -- flag ) { dup 0< swap 0= or not }
%sub ( x y -- z ) { negate ADD } ( bypass )
%equal ( x y -- flag ) { sub 0= }
%lesser ( x y -- flag ) { sub 0< }
%greater ( x y -- flag ) { sub 0> }
|000 @t $1
|100
#06 2-
#010e DEO
BRK
Chuck Moore also uses a pared down Forth for his custom minimal-instruction set processors. They are an inspiration for designing other minimal languages. For example, his latest designs have five-bit instructions, for 32 possible opcodes:
| Stack | DROP, DUP, OVER, PUSH, POP |
|---|---|
| Math | +, AND, XOR, NOT, 2*, 2/, multiply-step |
| Call | JUMP, CALL, RETURN, IF, -IF |
| Loop | NEXT, UNEXT |
| Register | A, A!, B! |
| Memory | @, !, @+, !+, @B, !B, @P, !P |
| NO-OP | . |
- Forth Tutorial
- Original lbforth
- Forth Methodology
- Forth Primitives
- Language for Thoughtful Programming
- Forth History
- Design Decisions in the Forth Kernel
- 3 Instructions Forth
- Linear Logic and Permutation Stacks
- The Language That Writes Itself, by Ratfactor
- Thoughts, by Felix Winkelmann
Live frogs are just very different
than dead frogs.
incoming: firth notation reversible computing postscript uxntal notation uxn devlog 2026 2024 malleable computing