programming languages

A programming language is a system of notation for writing computer programs.

I've collected here a handful of notes on the various languages that I've had the opportunity to use in the past.

Nowadays, my focus is principally on concatenative languages, namely Uxntal. In concatenative languages all expressions denote functions, and the juxtaposition of expressions denotes function composition, which I found was a way of programming that most resonated with how I think.

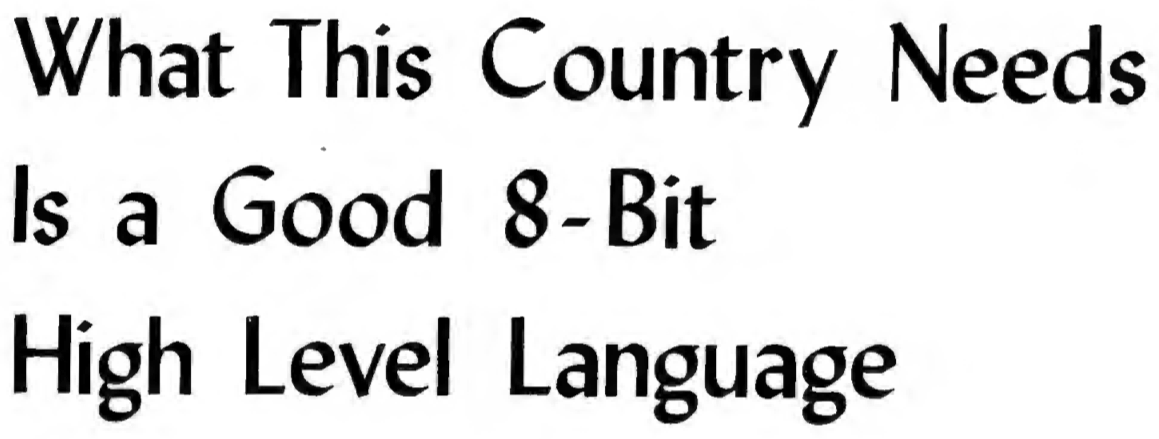
Point-free programming is a programming paradigm in which function definitions do not identify the arguments on which they operate. Instead the definitions merely compose other functions, among which are combinators that manipulate the arguments.

Assembly languages have a strong correspondence between the operands and the architecture.

Imperative languages organize programs in procedures and subroutines.

A programming paradigm where instructions are given to the computer in a step-by-step manner, detailing how to achieve a desired result by explicitly changing the program's state.

Fizzbuzz, in BASIC.

1 REM This is a comment.
2 LET I:I+1, F:I%3=0, B:I%5=0
3 IF F PRINT "FIZZ";
4 IF B PRINT "BUZZ";
5 IF F+B=0 PRINT I;
6 PRINT ""
7 IF I<101 GOTO 2
8 END

Fizzbuzz, in C.

#include <stdio.h>
int main(void) {
	for (int i = 1; i <= 100; i++) {
		if (i % 15 == 0)
			printf("FizzBuzz\n");
		else if (i % 3 == 0)
			printf("Fizz\n");
		else if (i % 5 == 0)
			printf("Buzz\n");
		else
			printf("%d\n", i);
	}
	return 0;
}

Fizzbuzz, in Pascal.

program FizzBuzz;
var
	i : integer;
begin
	for i := 1 to 100 do
		if i mod 15 = 0 then
			writeln('FizzBuzz')
		else if i mod 3 = 0 then
			writeln('Fizz')
		else if i mod 5 = 0 then
			writeln('Buzz')
		else
			writeln(i)
	end.

Fizzbuzz, in Smalltalk-80.

| i fizz buzz |
i _ 1.
100 timesRepeat: [
	fizz _ i\\3=0.
	buzz _ i\\5=0.
	(fizz) ifTrue: [Transcript show: 'Fizz'].
	(buzz) ifTrue: [Transcript show: 'Buzz'].
	(fizz | buzz) ifFalse: [Transcript show: i printString].
	Transcript cr.
	i _ i + 1.
]

Fizzbuzz, in Hypercard.

on mouseUp
	put 1 into n
	put 1 into fizz
	put 1 into buzz
	repeat 100
		if fizz is 3 and buzz is 5 then
			put "FizzBuzz" into line n of background field "Output"
			put 0 into fizz
			put 0 into buzz
		else if fizz is 3 then
			put "Fizz" into line n of background field "Output"
			put 0 into fizz
		else if fizz is 5 then
			put "Buzz" into line n of background field "Output"
			put 0 into buzz
		else
			put n into line n of background field "Output"
		end if
		put n+1 into n
		put fizz+1 into fizz
		put buzz+1 into buzz
	end repeat
end mouseUp

Concatenative languages use juxtaposition of expressions for function composition.

The point-free programming paradigm is where function definitions do not identify the arguments on which they operate, all terms denote unary functions applied on a stack or a queue.

Fizzbuzz, in Uxntal.

#6400
@fizzbuzz ( n i -- )
	LITr 00
	DUP #03 DIVk MUL SUB ?{ INCr ;&f str/print }
	DUP #05 DIVk MUL SUB ?{ INCr ;&b str/print }
	LITr _{ JCNr dec/print } #0a18 DEO
	INC GTHk ?fizzbuzz
	POP2 BRK
		&f "Fizz $1 &b "Buzz $1
@dec/print ( n -- n )
	DUPk #0a DIV /d #0a DIVk MUL SUB &d #30 ADD #18 DEO JMP2r
@str/print ( s* -- )
	LDAk #18 DEO INC2 LDAk ?&print POP2 JMP2r

Rewriting languages are typically made of rules and an initial state.

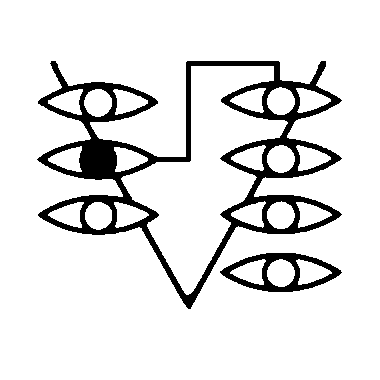
A program begins with a series of rules which define tokens to match, and the resulting transformation. When a rule consumes a specific token during the application, we'll call this token the reagent. When a rule utilizes a specific token that survives the rewrite, we'll call it the catalyst.

Fizzbuzz, in Modal.

<> ((print-word ?:) ?i ?f ?b) ((print-line \n) ?i ?f ?b)
<> ((print-line ?:) ?i ?f ?b) ((?i) (?f) (?b))
<> (100 ?f ?b) (done.)
<> (?i 3 5)    ((print-word FizzBuzz) ?i 0 0)
<> (?i 3 ?b)   ((print-word Fizz) ?i 0 ?b)
<> (?i ?f 5)   ((print-word Buzz) ?i ?f 0)
<> (?i ?f ?b)  ((print-word ?i) ?i ?f ?b)
(0 0 0)

Fizzbuzz, in Fractran.

:: Fizz >
:: Buzz >
:: eval #i^100 >
:: eval f^3 b^5 > incr Fizz Buzz
:: eval f^3 > incr Fizz
:: eval b^5 > incr Buzz
:: eval > incr
:: incr > #i f b eval
incr

Pocket Rewriting, a multiset rewriting zine.
Horadric, a rewriting mailing list.

Functional languages rely on first-class functions, anonymous functions and immutability.

A programming paradigm in which function definitions are trees of expressions that map values to other values, rather than a sequence of imperative statements.

Fizzbuzz, in LISP 1.5.

(LETREC main
	(main λ (INPUT)
		(loop (QUOTE 1) (QUOTE 100)))
	(loop λ (x y v)
		(IF (LEQ x y)
			(loop (+ x (QUOTE 1)) y (fizzbuzz x))
			(QUOTE Completed)))
	(fizzbuzz λ (n)
		(IF (EQ (% n (QUOTE 15)) (QUOTE 0))
			(WRITE (QUOTE FizzBuzz))
			(IF (EQ (% n (QUOTE 3)) (QUOTE 0))
				(WRITE (QUOTE Fizz))
				(IF (EQ (% n (QUOTE 5)) (QUOTE 0))
					(WRITE (QUOTE Buzz))
					(WRITE n))))))

Neural nets languages use synthetic neurons as the base computational unit.

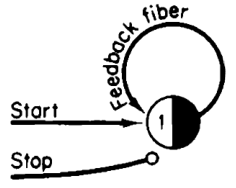
This is a simplistic model of the neuron that doesn't capture all of its properties and behavior but just enough to capture the way it performs computation.

Fizzbuzz, in McCulloch-Pitts neurons.

0*:
	1*: 2*: 3*: 4*: 5*: 6*: 7*: 8*: 9*: 0*.
fizz*: 
	*: *: fizz*.
buzz*: 
	*: *: *: *: buzz*.

Initialize 0*, fizz* & buzz*.

Graphical languages uses non-textual representation for programs.

A Methuselah is a small seed pattern of initial live cells that take a large number of generations in order to stabilize. A Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way.

Fizzbuzz, in Orca.

.aCa..Ca.........
1V9.0V4...2V*....
.C3......C5......
.0F0.....4F0.....
..."Fizz..."Buzz.
.2v0.....2v0.....
.V22K10..H.......
.0Y0"94..*/0a....