Belphegor's prime is the palindromic prime number 1000000000000066600000000000001 (1030 + 666 × 1014 + 1), a number which reads the same both backwards and forwards and is only divisible by itself and one.
A prime number cannot be divided by any other number, apart from itself and one.
| Number | Primes | ||
|---|---|---|---|
| 2 | 3 | 5 | |
| 6 | 1 | 1 | 0 |
| 375 | 0 | 1 | 3 |
| 2250 | 1 | 2 | 3 |
To find the prime factorization of a number, start by dividing the number by the first prime number 2 and continue dividing by 2 until you get a decimal or remainder. Then divide by 3, 5, 7, etc. until the only numbers left are prime numbers.
Multiplying two numbers is the same as adding the counts of each prime
factors, and division is the same as subtracting the counts. For example, using
numbers made up of the 3 first primes(2, 3, 5), 2250 is equal to 2^1 x
3^2 x 5^3.
Greatest Common Divisor
long gcd(long a, long b) {
while (b != 0) {
long t = b;
b = a % b, a = t;
}
return a;
}
Least Common Multiple
long lcm(long a, long b) {
return (a / gcd(a,b)) * b;
}
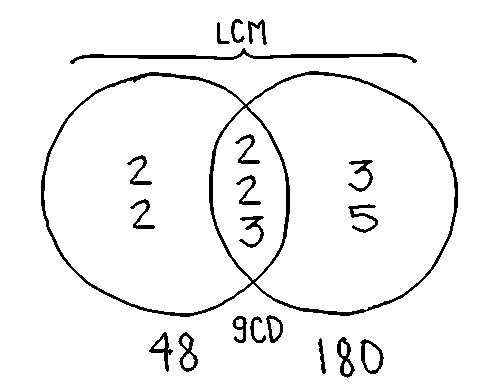
Using prime factorization, one can find the GCD and LCM of two numbers.
- 48 = 2^4 × 3
- 180 = 2^2 × 3^2 × 5
- LCM = 2^4 × 3^2 × 5 = 720
- GCD = 2^2 × 3 = 12
- Product = 720 × 12 = 8640
An interesting part of primes is the ability to encode data, values can be encoded as exponents to a number's prime factors, or as values to registers as in Fractran. For example, the letters of the word "HELLO" can be stored as ascii exponents to the first five primes:
| H | E | L | L | O |
| 2^72 | 3^69 | 5^76 | 7^76 | 11^79 |
The resulting number storing the values of each character of "HELLO":
1639531486723067852359816964623169016543137549 4122401687192804219102815235735638642399170444 5066082282398711507312101674742952521828622795 1778467808618104090241918575825850806280956250 0000000000000000000000000000000000000000000000 0000000000000000000000000
Extra letters can be appended by multiplying with a number reducible with the
following prime, for example * 13^33 would make our message
"HELLO!". Letters can also be removed by dividing by one of its factors, for
example / 3^69 would make our message "HLLO!".
Hexadecimal Primes Table
The 256 primes in hexadecimal, starting at 3:
0003 0005 0007 000b 000d 0011 0013 0017 001d 001f 0025 0029 002b 002f 0035 003b 003d 0043 0047 0049 004f 0053 0059 0061 0065 0067 006b 006d 0071 007f 0083 0089 008b 0095 0097 009d 00a3 00a7 00ad 00b3 00b5 00bf 00c1 00c5 00c7 00d3 00df 00e3 00e5 00e9 00ef 00f1 00fb 0101 0107 010d 010f 0115 0119 011b 0125 0133 0137 0139 013d 014b 0151 015b 015d 0161 0167 016f 0175 017b 017f 0185 018d 0191 0199 01a3 01a5 01af 01b1 01b7 01bb 01c1 01c9 01cd 01cf 01d3 01df 01e7 01eb 01f3 01f7 01fd 0209 020b 021d 0223 022d 0233 0239 023b 0241 024b 0251 0257 0259 025f 0265 0269 026b 0277 0281 0283 0287 028d 0293 0295 02a1 02a5 02ab 02b3 02bd 02c5 02cf 02d7 02dd 02e3 02e7 02ef 02f5 02f9 0301 0305 0313 031d 0329 032b 0335 0337 033b 033d 0347 0355 0359 035b 035f 036d 0371 0373 0377 038b 038f 0397 03a1 03a9 03ad 03b3 03b9 03c7 03cb 03d1 03d7 03df 03e5 03f1 03f5 03fb 03fd 0407 0409 040f 0419 041b 0425 0427 042d 043f 0443 0445 0449 044f 0455 045d 0463 0469 047f 0481 048b 0493 049d 04a3 04a9 04b1 04bd 04c1 04c7 04cd 04cf 04d5 04e1 04eb 04fd 04ff 0503 0509 050b 0511 0515 0517 051b 0527 0529 052f 0551 0557 055d 0565 0577 0581 058f 0593 0595 0599 059f 05a7 05ab 05ad 05b3 05bf 05c9 05cb 05cf 05d1 05d5 05db 05e7 05f3 05fb 0607 060d 0611 0617 061f 0623 062b 062f 063d 0641 0647 0649 064d 0653 0655
incoming: cccc lunar arithmetic fractran 2022 2021