A compiler assigns the symbols left, side and right to the prime numbers 2, 3 and 5. The product of left(2) and side(3) for the denominator, side(3) and right(5) for the numerator, result in the fraction 15/6.
Fractran is a computer architecture based entirely on the multiplication of fractions.
A prime is a number that can only be divided by itself one, since these numbers can't be divided, they can considered the DNA of other numbers. The factoring of a number into prime numbers, for example: 18 = 2 × 32, exposes values which Fractran utilizes as registers. There are two parts to a Fractran program:

The Accumulator
| Accumulator | Registers | |||
|---|---|---|---|---|
| r2 | r3 | r5 | r7 | |
| 6 | 1 | 1 | ||
| 18 | 1 | 2 | ||
| 1008 | 4 | 2 | 1 | |
| 5402250 | 1 | 2 | 3 | 4 |
The Accumulator is a single number whose prime factorization holds the value of registers(2, 3, 5, 7, 11, 13, 17, ..). For example, if the state of the accumulator is 1008(2⁴ × 3² × 7), r2 has the value 4, r3 has the value 2, r7 has the value 1, and all other registers are unassigned.
The Fraction
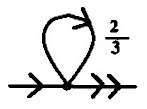
A Fraction represents an instruction that tests one or more registers by the prime factors of its numerator and denominator. To evaluate the result of a rule we take the the accumulator, if multiplying it by this fraction will give us an integer, we will update the accumulator with the result.
| 2/3 | 15/256 | 21/20 |
|---|---|---|
| (21)/(31) | (31 × 51)/(28) | (31 × 71)/(22 × 51) |
if(r3 >= 1){ r3 -= 1; r2 += 1; return; } |
if(r2 >= 8){ r2 -= 8; r3 += 1; r5 += 1; return; } |
if(r2 >= 2 && r5 >= 1){ r2 -= 2; r5 -= 1; r3 += 1; r7 += 1; return; } |
Operations become more readable when broken down into their primes. We can think of every prime number as having a register which can take on non-negative integer values. Each fraction is an instruction that operates on some of the registers.
A Notation
While Fractran is commonly reduced to just another opaque esoteric language, portraying it as such is doing a disservice to the relatively simple idea at its core and to the researchers who might otherwise benefit to venture deeper into a relatively unexplored field of computation.
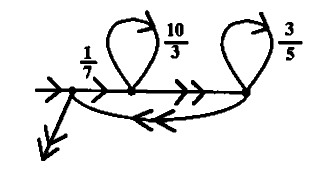
Wryl, who created Modal, demonstrated to me an interesting connection between Fractran and rewriting languages which is made clearer by using a notation where prime registers are automatically assigned names, and fractions are defined in terms of transformations of these names:
:: left side > right side 15/6 left.2 side.3 > side.3 right.5 AC 6 left side accumulator 00 6 × 15/6 = 15, side right result
This documentation will represent registers with names(x, y, foo-bar, baz,
..). Fractions will be written as rewrite rules starting with ::,
a left-side, a spacer(>) and a right-side. The notation indicates which
registers to replace on the denominator left-side, and what to replace them
with on the numerator right-side. Unlike John Conway's original specification
of Fractran, fractions are not reduced.
Multiset sounds too technical.
Dijkstra's bag, not technical enough.
Programming In Fractran
In a rule definition, which is a fraction where prime factorization is written as names, we find names to the left-side of the spacer(>) to be rewritten by names found on the right-side. Each new name is added to the dictionary and represented internally as a prime number.
:: > A rule with no left-side is a comment. :: flour sugar apples > apple-cake :: apples oranges cherries > fruit-salad :: fruit-salad apple-cake > fruit-cake sugar oranges apples cherries flour apples
Rules are tested in a sequence from the first to the last, when a rewrite rule gives us an integer when when multiplied by the accumulator, the accumulator is updated by the product of that multiplication, and search for the next rule starts back again from the beginning.
:: 7/30 flour.2 sugar.3 apples.5 > apple-cake.7 :: 17/715 apples.5 oranges.11 cherries.13 > fruit-salad.17 :: 19/119 apple-cake.7 fruit-salad.17 > fruit-cake.19 AC 21450 flour sugar apples apples oranges cherries 00 21450 × 7/30 = 5005, apples apple-cake oranges cherries 01 5005 × 17/715 = 119, apple-cake fruit-salad 02 119 × 19/119 = 19, fruit-cake
In other words, it helps to visualize the fractions in a program as a list of rewrite rules that tests the accumulator against its left-side, and starts back at the top of the list after updating the accumulator when it is a match, or keep going when it does not.
Fractran has a single operation, and can be explained in 10 seconds.
- For each fraction in a list for which the multiplication of the accumulator and the fraction is an integer, replace the accumulator by the result of that multiplication.
- Repeat this rule until no fraction in the list produces an integer when multiplied by the accumulator, then halt.
That's all!
Loops
Loops are a useful and common construct in programming, here is an example program in the imperative style that cycles through the four seasons until it reaches the autumn of the year two:
while(year++) {
for(season = 0; season < 4; season++) {
if(year == 2 && season == 3)
return print("Reached!");
}
}
To create a loop, a rewriting program relies on cycling back onto a term and the boundary of a loop is done by catching the ending case. Now, if we translate the above program into rewrite rules:
:: year year autumn > Reached! :: spring > summer > autumn > winter > spring year spring
Looking at the trace of the evaluation, we can see the following transformations:
AC 7, spring 01 7 × 11/7 = 11, summer 02 11 × 3/11 = 3, autumn 03 3 × 13/3 = 13, winter 04 13 × 14/13 = 14, year spring 01 14 × 11/7 = 22, year summer 02 22 × 3/11 = 6, year autumn 03 6 × 13/3 = 26, year winter 04 26 × 14/13 = 28, year^2 spring 01 28 × 11/7 = 44, year^2 summer 02 44 × 3/11 = 12, year^2 autumn 00 12 × 5/12 = 5, Reached!
Logic
Binary logic is typically implemented as multiple rules, where each is a potential location in the truth table:
:: x y and? > true :: x and? > false :: y and? > false :: and? > false :: x y or? > true :: x or? > true :: y or? > true :: or? > false :: x y xor? > false :: x xor? > true :: y xor? > true :: xor? > false :: true not? > false :: false not? > true AC 30, x y and? 00 30 × 7/30 = 7, true
The comparison operations are implemented using a loop that drains the registers until only the offset remains:
:: x y gth? > gth? :: x gth? > true :: gth? > false :: x y lth? > lth? :: y lth? > true :: lth? > false :: x y equ? > equ? :: x equ? > false :: y equ? > false :: equ? > true :: x y neq? > neq? :: x neq? > true :: y neq? > true :: neq? > false AC 2160, x^4 y^3 gth? 00 2160 × 5/30 = 360, x^3 y^2 gth? 00 360 × 5/30 = 60, x^2 y gth? 00 60 × 5/30 = 10, x gth? 01 10 × 7/10 = 7, true
Arithmetic
The sum of two registers(x+y) can be reached by writing the result in a third register(sum):
:: x add > add sum :: y add > add sum :: add > AC 2352, x^4 add y^2 00 2352 × 15/6 = 5880, x^3 add sum y^2 00 5880 × 15/6 = 14700, x^2 add sum^2 y^2 00 14700 × 15/6 = 36750, x add sum^3 y^2 00 36750 × 15/6 = 91875, add sum^4 y^2 01 91875 × 15/21 = 65625, add sum^5 y 01 65625 × 15/21 = 46875, add sum^6 02 46875 × 1/3 = 15625, sum^6
Alternatively, the result can also be reached by moving the value of one register into the other:
:: y > x AC 144 x^4 y^2 00 144 × 2/3 = 96, x^5 y 00 96 × 2/3 = 64, x^6
The difference between two registers(x-y) can be reached by consuming the value of two registers at once, and moving the remains into a third(pos) and fourth(neg) to get the signed result:
:: x y sub > sub :: x sub > sub pos :: y sub > sub neg :: sub > AC 58320, x^4 y^6 sub 00 58320 × 5/30 = 9720, x^3 y^5 sub 00 9720 × 5/30 = 1620, x^2 y^4 sub 00 1620 × 5/30 = 270, x y^3 sub 00 270 × 5/30 = 45, y^2 sub 02 45 × 55/15 = 165, y sub neg 02 165 × 55/15 = 605, sub neg^2 03 605 × 1/5 = 121, neg^2
Alternatively, the result can also be reached by consuming the value of two registers at once, and moving the remains to the first if we want the result inside x:
:: x y > :: y > x AC 576 x^6 y^2 00 576 × 1/6 = 96, x^5 y 00 96 × 1/6 = 16, x^4
The doubling of a register(x*2) is a matter of incrementing an output register twice for each input register values:
:: x double > res res double :: double > AC 48, x^4 double 00 48 × 75/6 = 600, x^3 double res^2 00 600 × 75/6 = 7500, x^2 double res^4 00 7500 × 75/6 = 93750, x double res^6 00 93750 × 75/6 = 1171875, double res^8 01 1171875 × 1/3 = 390625, res^8
The halving of a register(x/2) is a matter of decrementing an input register twice for each output register value:
:: x x half > res half :: half > AC 48, x^4 half 00 48 × 15/12 = 60, x^2 half res 00 60 × 15/12 = 75, half res^2 01 75 × 1/3 = 25, res^2
A similar set of rules can check if a register is odd or even:
:: x x even? > even? :: x even? > false :: even? > true AC 384, x^7 even? 00 384 × 3/12 = 6, x even? 01 6 × 5/6 = 5, false
The product is reached from a series of additions, by copying the input register, into a temporary register and third result register.
:: z i > x i :: i > :: x y > y z res :: y > i :: x > AC 675, x^3 y^2 02 675 × 70/15 = 3150, res x^2 y^2 z 02 3150 × 70/15 = 14700, res^2 x y^2 z^2 02 14700 × 70/15 = 68600, res^3 y^2 z^3 03 68600 × 11/5 = 150920, res^3 y z^3 i 00 150920 × 33/77 = 11880, res^3 x^3 y i 01 11880 × 1/11 = 1080, res^3 x^3 y 02 1080 × 70/15 = 5040, res^4 x^2 y z 02 5040 × 70/15 = 23520, res^5 x y z^2 02 23520 × 70/15 = 109760, res^6 y z^3 03 109760 × 11/5 = 241472, res^6 z^3 i 00 241472 × 33/77 = 19008, res^6 x^3 i 01 19008 × 1/11 = 1728, res^6 x^3 04 1728 × 1/3 = 64, res^6
Example: Fibonacci
Let's have a look at a real program to generate the Fibonacci Sequence(1, 1, 2, 3, 5, 8, 13, 21, 34..). This program uses catalysts(fib, fib.shift, fib.move) to keep the program state which has 3 phases(shift, move and back to fib) and ensures the correct evaluation order:
:: fib n last > fib n B :: fib n res > fib n A B :: fib n > fibrec :: fibrec A > fibrec last :: fibrec B > fibrec res :: fibrec > fib :: last > AC 31590, res n^5 last fib .. 06 41600000000 × 1/5 = 106496, res^13 fib
31590 : 429/195 3003/78 17/39 85/119 34/187 13/17 1/5
Example: Factorial
Let's have a look at something a bit more advanced, the function to generate the 5th Factorial number from the sequence(1, 2, 6, 24, 120..). This program uses a multiplication portion, and a series of rules to move between each number in the sequence:
:: fac a i > fac n i :: i > :: fac n y > fac res a y :: fac y > fac i :: fac > :: res > y :: n n > fac n AC 23750, fac n^4 y .. 05 125829120 × 2/3 = 83886080, y^24 n
23750 : 2755/12673 1/29 2622/190 551/38 1/19 2/3 95/25
This solution was contributed by TARDIInsanity.
Operator Precedence
To find the result of 3*(4+5)-6, in which a specific sequence of
operation is needed to find the correct answer, the
order in which operators will be evaluated can be specified with the order in which the rules are created:
:: +5 > x^5 :: *3 x > *3 y^3 :: *3 > :: -6 y^6 > x^4 +5 *3 -6 AC 27664, x^4 +5 *3 -6 00 27664 × 32/7 = 126464, x^9 *3 -6 01 126464 × 351/26 = 1883522578791789, y^27 *3 -6 02 1883522578791789 × 1/13 = 144886352214753, y^27 -6 03 144886352214753 × 1/13851 = 10460353203, y^21
A Stack Machine
A stack-machine can be implemented in Fractran, by allocating a number of registers to store the items in the stack. We can push a value stored in x to the top of the stack by shifting the content from one register to the next.
:: push > move-de :: move-de d > move-de e :: move-de > move-cd :: move-cd c > move-cd d :: move-cd > move-bc :: move-bc b > move-bc c :: move-bc > move-ab :: move-ab a > move-ab b :: move-ab > move-xa :: move-xa x > move-xa a :: move-xa > :: a) > push x^1 b) :: b) > push x^2 c) :: c) > push x^3 a)
In that same way, we can pop, and store in x, the value at the top of the stack by shifting content the other way.
:: pop > move-ax :: move-ax a > move-ax x :: move-ax > move-ba :: move-ba b > move-ba a :: move-ba > move-cb :: move-cb c > move-cb b :: move-cb > move-dc :: move-dc d > move-dc c :: move-dc > move-ed :: move-ed e > move-ed d :: move-ed > a^1 b^2 c^3 pop
Example: Tic-Tac-Toe
Fractran's output capability is limited to the resulting accumulator at the end of an evaluation. The advantage of symbolic rewriting is that registers are already assigned names, so we shall print those instead. As for input, we can type in new symbol tokens and appending their value to the accumulator between evaluations. We can implement a tic-tac-toe in a mere 16 rules:
:: > Reserve the first registers for the player moves
:: x#a o#a x#b o#b x#c o#c
:: x#d o#d x#e o#e x#f o#f
:: x#g o#g x#h o#h x#i o#i
:: > This register remains active until the game ends
game
:: > A symbol to draw the value of registers in a grid
"
Set move in the format x#a, o#b, x#c, etc:
a b c | {x#a o#a .} {x#b o#b .} {x#c o#c .}
d e f | {x#d o#d .} {x#e o#e .} {x#f o#f .}
g h i | {x#g o#g .} {x#h o#h .} {x#i o#i .}
"
:: > Rules for each possible victory states
:: game x#a x#b x#c > x#a x#b x#c "Player X wins!"
:: game o#a o#b o#c > o#a o#b o#c "Player O wins!"
:: game x#d x#e x#f > x#d x#e x#f "Player X wins!"
:: game o#d o#e o#f > o#d o#e o#f "Player O wins!"
:: game x#g x#h x#i > x#g x#h x#i "Player X wins!"
:: game o#g o#h o#i > o#g o#h o#i "Player O wins!"
:: game x#a x#e x#i > x#a x#e x#i "Player X wins!"
:: game o#a o#e o#i > o#a o#e o#i "Player O wins!"
:: game x#g x#e x#c > x#g x#e x#c "Player X wins!"
:: game o#g o#e o#c > o#g o#e o#c "Player O wins!"
:: game x#a x#d x#g > x#a x#d x#g "Player X wins!"
:: game o#a o#d o#g > o#a o#d o#g "Player O wins!"
:: game x#b x#e x#h > x#b x#e x#h "Player X wins!"
:: game o#b o#e o#h > o#b o#e o#h "Player O wins!"
:: game x#c x#f x#i > x#c x#f x#i "Player X wins!"
:: game o#c o#f o#i > o#c o#f o#i "Player O wins!"
Program don't need to specify anything other than these 16 rules, as players can already input their moves in the format of its register names: x#a, o#b, x#c, etc.
Set move in the format x#a, o#b, x#c, etc: a b c | x o o d e f | . x . g h i | . . x Player X wins!
A Fractran program specifies the wiring and logic of an interactive application, registers point to symbols in memory and so the bytecode itself is never localized as these strings reside in the application's front-end far from its logic.
Example: Fizzbuzz
Alternatively to getting the resulting program state at the end of an evaluation, we can emit the accumulator at a specific rate during the evaluation by checking if a register is active or not.
:: > Reserve the first registers for the increments and base-10
:: +5 +3
:: 1# 2# 3# 4# 5# 6# 7# 8# 9# 0
:: 1 2 3 4 5 6 7 8 9
:: > Leave the printing register for no more than one rewrite
:: print: fizz >
:: print: buzz >
:: print: fizzbuzz >
:: print: "{1# 2# 3# 4# 5# 6# 7# 8# 9# 0}{1 2 3 4 5 6 7 8 9}" >
:: > Fizzbuzz logic
:: eval +3 +3 +3 +5 +5 +5 +5 +5 > print: fizzbuzz
:: eval +3 +3 +3 > print: fizz
:: eval +5 +5 +5 +5 +5 > print: buzz
:: eval > print: "{1# 2# 3# 4# 5# 6# 7# 8# 9# 0}{1 2 3 4 5 6 7 8 9}"
:: > Base-10 numbers
:: 1# 9 > 2# 0 +3 +5 eval
:: 2# 9 > 3# 0 +3 +5 eval
:: 3# 9 > 4# 0 +3 +5 eval
:: 4# 9 > 5# 0 +3 +5 eval
:: 5# 9 > 6# 0 +3 +5 eval
:: 6# 9 > 7# 0 +3 +5 eval
:: 7# 9 > 8# 0 +3 +5 eval
:: 8# 9 > 9# 0 +3 +5 eval
:: 9# 9 >
:: 0 > 1 +3 +5 eval
:: 1 > 2 +3 +5 eval
:: 2 > 3 +3 +5 eval
:: 3 > 4 +3 +5 eval
:: 4 > 5 +3 +5 eval
:: 5 > 6 +3 +5 eval
:: 6 > 7 +3 +5 eval
:: 7 > 8 +3 +5 eval
:: 8 > 9 +3 +5 eval
:: 9 > 1# 0 +3 +5 eval
:: > The initial state
0
During the evaluation, these 27 fractions will toggle r79(print:) giving us a trigger when the accumulator state might be read. This is demonstrated here as an alternative approach for emitting programs and debugging where the runtime is masking lower registers to the printing register.
07 25338 × 7979/103 = 1962834 01 07 159444 × 7979/103 = 12351492 02 05 1045656 × 6557/2781 = 2465432 fizz 07 262032 × 7979/103 = 20298576 04 06 1750176 × 7031/3296 = 3733461 buzz 05 339282 × 6557/2781 = 799954 fizz 07 82812 × 7979/103 = 6415116 07 07 526536 × 7979/103 = 40788648 08 05 3248208 × 6557/2781 = 7658576 fizz 06 1829280 × 7031/3296 = 3902205 buzz 07 380070 × 7979/103 = 29442510 11 05 2391660 × 6557/2781 = 5639020 fizz 07 580920 × 7979/103 = 45001560 13 07 3930480 × 7979/103 = 304478640 14 04 26252640 × 7663/88992 = 2260585 fizzbuzz 07 188490 × 7979/103 = 14601570 16 07 1242180 × 7979/103 = 96226740 17 05 7898040 × 6557/2781 = 18621880 fizz ..
To explore further, try running these examples yourself:

Reduction & Catalysts
Conway's Fractran traditionally compares the accumulator against reduced fractions, but computationally-speaking, getting to the gcd of a fraction does little more than getting rid of otherwise valuable information used during comparison to match against a restricted set of fractions. The support for catalysts, symbols found on both sides of a rewrite rule, makes for a simpler and faster implementation.
:: 15/6 red green > blue green :: 5/2 red > blue red green
These two fractions are not equal and reducing the first into the
second, eliminates the capability to match against it only when the
catalyst green is present in the accumulator.
Deadcode Elimination
An unreachable rule is created when a rule's left-hand side is part of the left-hand side of a rule below it:
:: foo > baz :: foo bar > baz foo bar
For a rule to be reachable, all the symbols in the left-hand side must be present in either the right-hand side of an other valid rule, or in the accumulator.
:: violet > red :: purple > violet violet
Rules that are unreachable are considered comments and should not be part of the ruleset during evaluation.
Exhaustive Rules
When moving values between registers, each move takes one rewriting and thus can quickly become computationally expensive:
:: a > res :: b > res AC 1000, a^3 b^3 00 1000 × 3/2 = 1500, a^2 res b^3 00 1500 × 3/2 = 2250, a res^2 b^3 00 2250 × 3/2 = 3375, res^3 b^3 01 3375 × 3/5 = 2025, res^4 b^2 01 2025 × 3/5 = 1215, res^5 b 01 1215 × 3/5 = 729, res^6 Completed in 6 steps.
A rule with a right-hand side that does not include symbols present in any of the left-hand sides of the rules above it can be run exhaustively and perform many applications without having to look for the next applicable rule:
AC 1000, a^3 b^3 00 1000 × 3/2 = 3375, res^3 b^3 01 3375 × 3/5 = 729, res^6 Completed in 2 steps.
Reversibility
Fractran operators are reversible, meaning that a some programs can run backward to their original state. Evaluation is undone by applying rules and inverting their numerator and denominator, or right and left sides.
AC 19, fruit-cake 02 19 × 119/19 = 119, apple-cake fruit-salad 01 119 × 715/17 = 5005, apples apple-cake oranges cherries 00 5005 × 30/7 = 21450, apples apples flour sugar oranges cherries
For a program to be reversible, two rules may not share identical numerators or denominators. The implementation of a reversible CNOT logic gate differs from the non-reversible logic gates in that we cannot rely on the absence of registers, rules must contain symbols for their absence:
:: c+ t+ cnot > c+ t- cnot :: c+ t- cnot > c+ t+ cnot :: c- t+ cnot > c- t+ cnot :: c- t- cnot > c- t- cnot

Implementation
A basic implementation of the runtime core is a mere 20 lines:
cc framin.c -o framin view raw
An implementation of the full symbolic runtime is about 300 lines:
cc fractran.c -o fractran view raw
The wise marvels at the commonplace.Confucius
- Fractran Interpreter(C89), used for this documentation.
- Fractran Interpreter(Web)
- Intro to Fractran
- Remembering John Conway
- On Esolang
incoming: pocket rewriting tote phutball firth binary primes fractions reversible computing rewriting thue bagel 2024 2021 malleable computing