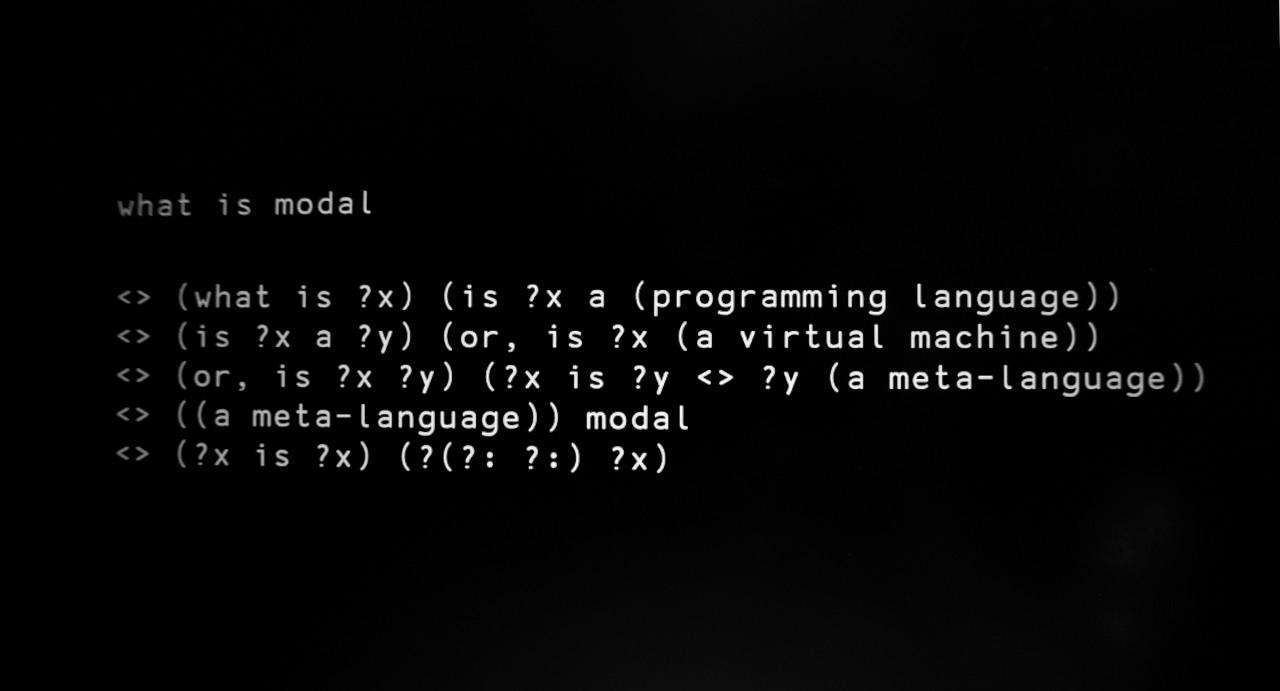
Modal is a programming language based on string rewriting.

Modal programs are represented as a series of substitution rules, applied to a given tree which gets continually modified until no rules match any given part of the tree. The principale elements of modal are:

• Rules: <> left right
• Registers: ?x, ?y, ?z
• Trees: word, (a tuple), a (nested (list))

The documentation below displays the examples as a series of rules, followed by the rewriting steps in the following format:

<> A rule

.. The input program
04 The result of applying rule #4
-1 The result of applying a lambda

Modal's evaluation model is based on scanning from left-to-right across a string that represents a serialized tree. We only match from the start of the string, and if we can't find a rule that matches, we move one token or subtree forward. All rules match against the start of the string, and if one matches, the matched pattern is erased, and the right-hand side of the rule is written to the end of the string.

Rules

To define a new rule, start with <>, followed by a left and a right statement, which is either a word, or a tree. The program evaluation starts at the first character of the string and walks through to the end trying to match a transformation rule from that location:

<> hello (good bye)  This is a rule

.. hello world       This is program data
00 good bye world    This is the result

Rules can be also be undefined using the >< operation that will try matching a previously declared rule's left statement:

<> cat owl
<> owl bat
<> owl rat
>< owl

.. cat 
00 owl 
02 rat

Modal is homoiconic, meaning that any string is a potential program and new rules can be composed directly during the evaluation. For instance, here is a rule that defines a new rules definition infix syntax:

<> (?x -> ?y) (<> ?x ?y)
fruit_a -> apple
fruit_b -> banana
(apple banana) -> fruit-salad

.. fruit_a fruit_b
01 apple fruit_b
02 apple banana
03 fruit-salad

Registers

Registers are single-character identifiers bound to an address in a pattern used in rewriting:

<> (copy ?a) (?a ?a)

.. copy cat
00 cat cat

When a register is used in a pattern, and when we try to match a given tree with a pattern, each register is bound to a corresponding an address to the left of a rule, and referenced to the right:

<> (swap ?x ?y) (?y ?x)

.. (swap fox rat)
00 (rat fox)

When a register appears more than once in a rule, each instance is bound to the first address, but differently named registers can still match on the same pattern:

<> ((?x ?x ?x)) match3
<> ((?x ?y)) match2

.. (fox fox fox) (bat bat) (bat cat)
00 match3 (bat bat) (bat cat)
01 match3 match2 (bat cat)
01 match3 match2 match2

Trees

Trees can be found in rules and program data, they include words, registers and nested trees. Rules can match specific trees and rewrite their content in a new sequence.

<> (rotate ?x (?y) ?z) (?y (?z) ?x)

.. rotate foo (bar) baz
00 bar (baz) foo

An efficient way to represent an array is to store information in nested lists, it allows for rules to target specific segments of the list, similarly to Lisp's car and cdr primitives. To print each element of such a structure, we can use the following recursive rules:

<> (putrec (?: ?x)) (putrec ?: ?x)
<> ((putrec (?:))) (?:)

.. (putrec (a (b (c (d (e))))))
00 (putrec (b (c (d (e)))))
00 (putrec (c (d (e))))
00 (putrec (d (e)))
00 (putrec (e))
01 

> abcde

Logic

Let us build a logic system, starting by comparing two registers:

<> (eq ?x ?x) (#t)
<> (eq ?x ?y) (#f)

.. (eq fox bat)
01 (#f)

We can implement the truth tables by defining each case:

<> (and #t #t) #t <> (or #t #t) #t 
<> (and #t #f) #f <> (or #t #f) #t
<> (and #f #t) #f <> (or #f #t) #t 
<> (and #f #f) #f <> (or #f #f) #f
<> (not #t) #f    <> (not #f) #t

.. (or #f #t)
08 (#t)

Building on the comparison rule above, we can write conditionals with a ternary statement:

<> (ife #t ?t ?f) (?t)
<> (ife #f ?t ?f) (?f)
<> (print ?:) (?:)

.. ife #f (print True!) (print False!)
13 (print False!)
14 ()

Types

Understanding how to use typeguard to reach a specific evaluation order is important to become proficient with Modal. Creating a type system is merely a matter of creating stricter rules expecting a specific grammar. Notice in the example below, how join-strings expects to match two String typed words. Without typed inputs, the rule is not matched.

<> (join-strings (String ?x) (String ?y)) (?x?y)

.. join-strings (String foo) (String bar)
00 foobar

Lambdas

A lambda is created by using the ?(body) special register. Rules created that way exist only for the length of one rewrite and must match what is found immediately after:

.. ?((?x ?y) (?y ?x)) foo bar
-1 bar foo

Outgoing Events

Sending a message is done with the ?: special register, it sends a word or a tree to be handled by a device:

<> (print ?:) (?:)

.. print (hello world\n)

hello world

Incoming Events

Similarly, listening to incoming messages is done with the ?~ special register:

<> (?: print) (?:)
<> (READ ?~) ((You said: ?~ \n) print)

.. (READ stdin)

You said: 

Special Registers Reference

The ?* special register explodes a token or tuple into a nested list, and the ?^ register to join it back into a single word. Notice how the following program makes use the List type to ensure a specific evaluation order:

<> (reverse List () ?^) (?^)
<> (reverse (?*)) (reverse List (?*) ())
<> (reverse List (?x ?y) ?z) (reverse List ?y (?x ?z))

.. (reverse (modal))
01 (reverse List (m (o (d (a (l ()))))) ())
02 (reverse List (o (d (a (l ())))) (m ()))
02 (reverse List (d (a (l ()))) (o (m ())))
02 (reverse List (a (l ())) (d (o (m ()))))
02 (reverse List (l ()) (a (d (o (m ())))))
02 (reverse List () (l (a (d (o (m ()))))))
00 (ladom)

sierpiński.modal

To review everything documented above, here is a small program that prints the Sierpiński triangle fractal:

?(?-) (Rules)

<> (* (. > (. ?x))) (* (. (. > ?x))) 
<> (. (. > (* ?x))) (* (. (* > ?x))) 

?(?-) (Physics)

<> (Tri > (?x ?y)) (Tri (?x > ?y))
<> (Tri (?x > (?y ?z))) (Tri (?x (?y > ?z)))
<> (?x (?y > (?z ?n))) (. (?y (?z > ?n)))
<> ((?x > ())) (< ())
<> (Tri < (* ?^)) (?(?: ?:) (*?^ \n))
<> ((?x < ?y)) (< (?x ?y))

?(?-) (Print)

<> (Tri.join ?x ?:) (Tri > ?x ?:)
<> (Tri.dup ?x ?^) (Tri.join ?x ?^)
<> (Tri < ?x) (Tri.dup (. ?x) (?x \n))

?(?* (Tri < (?*))) ...............*...............

Implementation

The language runtime can be implemented in about 300 lines.

cc modal.c -o modal view raw

• view sources, ANSI C.
• discord channel, in the concatenative server.
• Levels of Dynamic behavior in Modal
• This language is an original creation of wryl from 2018, who has courteously spent countless hours to help me progress with the language, much of the code above is derived from their research and merely made available here as to give this fantastic system a home on the internet.

Thuesday is a I/O specification for a string rewriting computer.

The philosophy behind Modal's I/O is that if it can't be done in rewriting alone, it's an I/O operation. Special registers are registers that do more than store a reference, they allow implementations to choose which special behavior is needed by the host platform, without impacting the core of the language. The specification below is for a collection of event handlers is called Thuesday.

ALU

The Thuesday system has a basic arithmetic engine(ALU) located in the I/O port that allows it to use numbers. As to not enforce a specific notation, assignment of values and operators is done entirely through numeral and I/O registers:

?((?: ?0 ?1 ?2) ?:) + 1 2 3 6     suffix notation 
?((?0 ?: ?1) ?:) 16 - 3     13    infix notation
?((?0 ?1 ?:) ?:) 12 10 *    120   postfix notation

<> (?0 ?1 `?:) ?:                 postfix generalized
12 34 `+                    46

Using what we have seen above, we can make sure that a token is a number by testing it against its value plus zero:

<> (?x ?x eq) (#t)
<> (?x ?y eq) (#f)
<> (is-number ?x) (?((?1 ?0 ?:) ?:) ?x 0 + ?x eq)

.. is-number 123 #t
.. is-number pig #f

The program can typeguard a against an adversary evaluation order by differentiating between intermediate results, to demonstrate this further, here is a postfix tail-recursive factorial function:

<> (?0 ?1 `?:) (Int ?:)

<> (?n factorial) (Int ?n Int 1 fact)
<> (Int 0 Int ?a fact) (?a)
<> (Int ?n Int ?a fact) (?n 1 `- ?n ?a `* fact)

.. 6 factorial 720

Viewport

Drawing is done using the same design as the ALU, where each numeric register represent an argument. Each argument in the shapes reference is ordered by register number, so the first word is bound to ?0, the second to ?1, and so on.

For example, the following program draws the Viznut bitart pattern:

<> (?0 ?1 `?:) ?:
<> (?2 ?0 ?1 ?: draw) ?:

<> ((?x ?y) Eval) (
	?x ?y `+ ?x ?y `- `& 24 `% 9 `> #ffffff `* ?x ?y pixel draw 
	(?x ?y) Viznut)

<> ((?x 256) Viznut) ()
<> ((256 ?y) Viznut) ((0 ?((?0 ?1 ?:) ?:) ?y 1 +) Eval)
<> ((?x ?y) Viznut) ((?((?0 ?1 ?:) ?:) ?x 1 + ?y) Eval)

?((?0 ?1 ?:) ?:) 256 256 size
(0 0) Viznut

Event Loop

Events are incoming events that trigger an evaluation, an evaluation will rewrite until a no rule match is reached.

Here is an example that creates a game loop and capture mouse and keyboard events to creates a basic drawing program:

<> (`?: ?0 ?1 ?2 ?3 (?4)) (?:)

?(?-) (Mouse handlers)

<> ((Last ?v ?w) handle-event (Touch (?x ?y ?z))) 
	((Last ?x ?y))
<> ((Last ?v ?w) handle-event (Move (?x ?y 1)))
	((Last ?x ?y) `line ?v ?w ?x ?y (#ff0000))

?(?-) (Keyboard events)

<> (handle-event (Key (?x q))) (?(?: ?:) quit)

?(?-) (Discard unknown events)

<> (handle-event ?x) ()

<> (on-event ?~) (handle-event ?~ on-event Any)

(Last 0 0) on-event Any

• view sources, C99(X11).

incoming fractran thuesday