XXIIVV
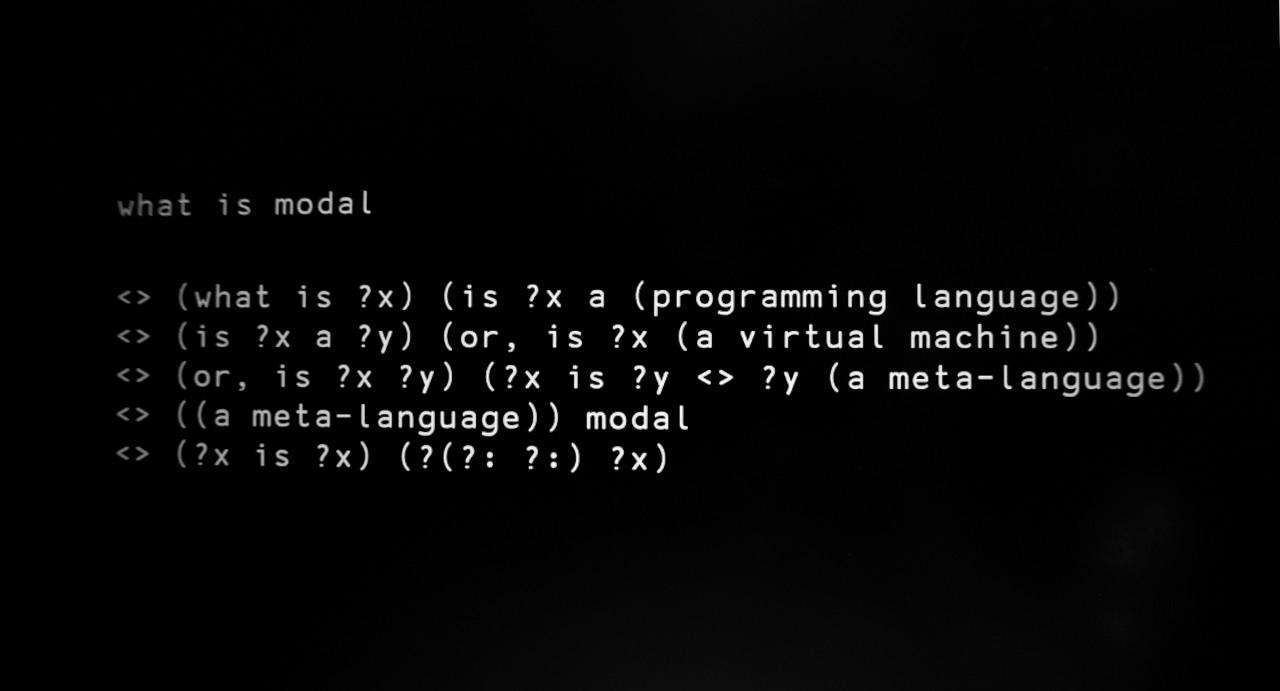
Modal In A Postcard
Modal In A Postcard

Modal is a programming language based on string rewriting.

Modal programs are represented as a series of substitution rules, applied to a given tree which gets continually modified until no rules match any given part of the tree. The principale elements of modal are:

The documentation below displays the examples as a series of rules, followed by the rewriting steps in the following format:

<> A rule

.. The input program
04 The result of applying rule #4
-1 The result of applying a lambda

Modal's evaluation model is based on scanning from left-to-right across a string that represents a serialized tree. We only match from the start of the string, and if we can't find a rule that matches, we move one token or subtree forward. All rules match against the start of the string, and if one matches, the matched pattern is erased, and the right-hand side of the rule is written to the end of the string.

Rules

To define a new rule, start with <>, followed by a left and a right statement, which is either a word, or a tree. The program evaluation starts at the first character of the string and walks through to the end trying to match a transformation rule from that location:

<> hello (good bye)  This is a rule

.. hello world       This is program data
00 good bye world    This is the result

Rules can be also be undefined using the >< operation that will try matching a previously declared rule's left statement:

<> cat (>< owl owl)
<> owl bat
<> owl rat

.. cat >< owl
>< owl bat
02 rat

Modal is homoiconic, meaning that any string is a potential program and new rules can be composed directly during the evaluation. For instance, here is a rule that defines a new rules definition infix syntax:

<> ((?x -> ?y)) (<> ?x ?y)
(a -> apple)
(b -> banana)
((apple banana) -> (fruit-salad))

.. a b
01 apple b
02 apple banana
03 fruit-salad

Registers

Registers are single-character identifiers bound to an address in a pattern used in rewriting:

<> (copy ?a) (?a ?a)

.. copy cat
00 cat cat

When a register is used in a pattern, and when we try to match a given tree with a pattern, each register is bound to a corresponding an address to the left of a rule, and referenced to the right:

<> (swap ?x ?y) (?y ?x)

.. (swap fox rat)
00 (rat fox)

When a register appears more than once in a rule, each instance is bound to the first address, but differently named registers can still match on the same pattern:

<> ((?x ?x ?x)) same
<> ((?x ?y)) different

.. (fox fox fox) (bat bat) (bat cat)
00 same (bat bat) (bat cat)
01 same different (bat cat)
01 same different different

Trees

Trees can be found in rules and program data, they include words, registers and nested trees. Rules can match specific trees and rewrite their content in a new sequence.

<> (rotate ?x (?y) ?z) (?y (?z) ?x)

.. rotate foo (bar) baz
00 bar (baz) foo

An efficient way to represent an array is to store information in nested lists, it allows for rules to target specific segments of the list, similarly to Lisp's car and cdr primitives. To print each element of such a structure, we can use the following recursive rules:

<> (putrec (?: ?x)) (putrec ?: ?x)
<> ((putrec (?:))) (?:)

.. (putrec (a (b (c (d (e))))))
00 (putrec (b (c (d (e)))))
00 (putrec (c (d (e))))
00 (putrec (d (e)))
00 (putrec (e))
01 

> abcde
modal(adj.): of, or relating to structure as opposed to substance.

Special Registers

Special registers are registers that do more than simply store a reference, they allow implementations to choose which special behavior is needed by the host platform, without impacting the core of the language:

Substrings
Explode token?(?* ?*) abca (b (c ()))
Explode tuple?(?* ?*) (abc def ghi)abc (def (ghi ()))
Unpack?(?. ?.) (abc def)abc def
Join?(?^ ?^) (abc def ghi)abcdefghi
IO
Read?~Read from devices
Send?:Send to devices

A lambda is created by using the ?(body) special register. Rules created that way exist only for the length of one rewrite and must match what is found immediately after: 

.. ?((?x ?y) (?y ?x)) foo bar
-1 bar foo

Explode a token or tuple, into a nested list with the ?* special register, notice how the following program makes use the List type to ensure a specific evaluation order:

<> (reverse List () ?^) (?^)
<> (reverse (?*)) (reverse List (?*) ())
<> (reverse List (?x ?y) ?z) (reverse List ?y (?x ?z))

.. (reverse (modal))
01 (reverse List (m (o (d (a (l ()))))) ())
02 (reverse List (o (d (a (l ())))) (m ()))
02 (reverse List (d (a (l ()))) (o (m ())))
02 (reverse List (a (l ())) (d (o (m ()))))
02 (reverse List (l ()) (a (d (o (m ())))))
02 (reverse List () (l (a (d (o (m ()))))))
00 (ladom)

Sending a message to a device is done with the ?: special register, it sends a word or a tree to be handled by a device:

<> (print ?:) (?:)

.. print (hello world\n)

hello world

Similarly, reading an incoming message from a device is done with the ?~ special register:

<> (?: print) (?:)
<> (READ ?~) ((You said: ?~ \n) print)

.. (READ stdin)

You said:

Type Systems

Understanding how to use types to guard rules for specific evaluation order is important to become proficient with Modal. Creating a type system is merely a matter of creating stricter rules expecting a specific grammar. Notice in the example below, how join-strings expects to match two String typed words. Without typed inputs, the rule is not matched.

<> (join-strings (String ?x) (String ?y)) (?x?y)

.. join-strings (String foo) (String bar)
00 foobar

Logic

Let us build a logic system, starting by comparing two registers:

<> (eq ?x ?x) (#t)
<> (eq ?x ?y) (#f)

.. (eq fox bat)
01 (#f)

We can implement the truth tables by defining each case:

<> (and #t #t) #t <> (or #t #t) #t 
<> (and #t #f) #f <> (or #t #f) #t
<> (and #f #t) #f <> (or #f #t) #t 
<> (and #f #f) #f <> (or #f #f) #f
<> (not #t) #f    <> (not #f) #t

.. (or #f #t)
08 (#t)

Building on the comparison rule above, we can write conditionals with a ternary statement: 

<> (ife #t ?t ?f) (?t)
<> (ife #f ?t ?f) (?f)
<> (print ?:) (?:)

.. ife #f (print True!) (print False!)
13 (print False!)
14 ()

Arithmetic

The language does not accommodate for any specific numerical system, but allows for the notion of numbers to be implemented with Peano Numerals:

<> (add (s ?x) (s ?y)) (s (add ?x (s ?y)))
<> (add (s ?x) (0)) (s ?x)
<> (add (0) (s ?y)) (s ?y)
<> (add (0) (0)) (0)
<> (sub (s ?x) (s ?y)) (sub ?x ?y)
<> (sub (s ?x) (0)) (s ?x)
<> (sub (0) (s ?y)) (s ?y)
<> (sub (0) (0)) (0)
<> (mul (s ?x) (s ?y)) (add (s ?x) (mul (s ?x) (sub (s ?y) (s (0)))))
<> (mul (s ?x) (s (0))) (s ?x)
<> (mul (s (0)) (s ?y)) (s ?y)
<> (mul (s ?x) (0)) (0)
<> (mul (0) (s ?x)) (0)

To convert from prefix notation to infix: 

<> (?x + ?y) (add ?x ?y)
<> (?x - ?y) (sub ?x ?y)
<> (?x * ?y) (mul ?x ?y)

Altogether, we have enough parts to implement factorial: 

<> (factorial (s (0))) ((s (0)))
<> (factorial (s ?x)) (((s ?x) * factorial ((s ?x) - (s (0)))))

factorial (s (s (s (s (s (0))))))

Binary

Prefix rules to increment a binary number:

<> (inc (0 ?x)) ((1 ?x))
<> (inc (1 ?x)) ((0 inc ?x))
<> (inc ()) ((1 ()))

?(?-) (Count to 0x7f)

<> (> increc (1 (1 (1 (1 ()))))) (done.)
<> (> increc ?i) (> (inc ?i wait) increc)
<> (> (?i wait) increc) (> increc ?i)

> increc ()

Mimics

We can use rules to define entire languages, Modal enforces no specific notation, for example, we could easily make a combinatory logic playground:

<> (M ?x) (?x ?x)
<> (KI ?x ?y) (?y)
<> (T ?x ?y) (?y ?y)
<> (W ?x ?y) (?x ?y ?y)
<> (K ?x ?y) (?x)
<> (C ?x ?y ?z) (?x ?z ?y)
<> (B ?x ?y ?z) (?x (?y ?z))
<> (I ?x) (?x)
<> (S ?x ?y ?z) (?x ?z (?y ?z))

.. C KI x y z
05 KI y x z
01 x z

Any choice made in regard to syntax is completely arbitrary. To demonstrate, the following code defines a concatenative syntax:

<> (?x dup) (?x ?x)
<> (?x ?y swap) (?y ?x)
<> (?x pop) ()

.. (1 2 3) (4 5 6) swap pop dup
01 (4 5 6) (1 2 3) pop dup
02 (4 5 6) dup
00 (4 5 6) (4 5 6)

sierpiński.modal

To review everything documented above, here is a small program that prints the Sierpiński triangle fractal:

?(?-) (Rules)

<> (* (. > (. ?x))) (* (. (. > ?x))) 
<> (. (. > (* ?x))) (* (. (* > ?x))) 

?(?-) (Physics)

<> (Tri > (?x ?y)) (Tri (?x > ?y))
<> (Tri (?x > (?y ?z))) (Tri (?x (?y > ?z)))
<> (?x (?y > (?z ?n))) (. (?y (?z > ?n)))
<> ((?x > ())) (< ())
<> (Tri < (* ?^)) (?(?: ?:) (*?^ \n))
<> ((?x < ?y)) (< (?x ?y))

?(?-) (Print)

<> (Tri.join ?x ?:) (Tri > ?x ?:)
<> (Tri.dup ?x ?^) (Tri.join ?x ?^)
<> (Tri < ?x) (Tri.dup (. ?x) (?x \n))

?(?* (Tri < (?*))) ...............*...............

Implementation

The Modal runtime can be implemented in about 300 lines of ANSI C.

cc modal.c -o modal view raw